Usually when we talk about software performance we face two kinds of problems. First, the system is given while the load is going to increase. In this case we want to know how the response time could change, how many servers we need to add to handle load. The second is when we’re trying to improve system performance. Considering the load as constant, we want to know how to reduce the response time, what changes could bring the most significant benefit and lower the infrastructure costs. This article is a gentle introduction to Queueing Theory that could help to in both cases.

Queuing theory terminology

First of all, let’s look on how the queuing theory models any system.

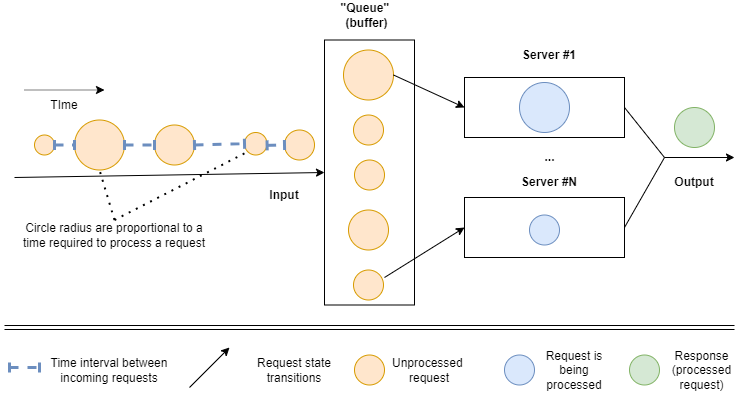
Requests arrive into a system with some random intervals between them. The time between two requests arrival in a row is called inter-arrival time. The inter-arrival time follows some distribution that doesn’t change over time. The average number of arrivals over some time period is called arrival rate and it’s denoted by a greek letter lambda($(\lambda)$). Once the request arrives, it may get into a “queue” where it waits for a free server. The time spent by a request in the queue is called queue waiting time. Once there’s a free server, a request processing starts. In the queuing theory server is something that do some work: in the context of the supermarket server is a cashier while in the software context it’s a single CPU core. Different requests require different amounts of wall-clock time for processing. The time between start of the request processing and the finish of request processing is called service time. Service time doesn’t include time spent in the queue. Request processing time follows some distribution that doesn’t change over time. The reciprocal of the average service time is called service rate and it’s denoted by greek letter mu ($(\mu$)). Service rate shows the average number of requests system can handle during the given time interval, for example in one minute. Once a request processing is finished, it leaves the system. For a web application case, this means that the response is sent back. The time between request arrival and sending response back is called time in the system or response time.

There’s subtle difference between queuing theory terminology and concepts that we use in the software domain, still under some circumstances we may use them interchangeable. Response time is measured on the client side. It’s time between sending a request and receiving a response. Hence, usually response time include network round trip time. Processing time is measured on the server side. It’s time between last byte of request received and the first byte of request send. 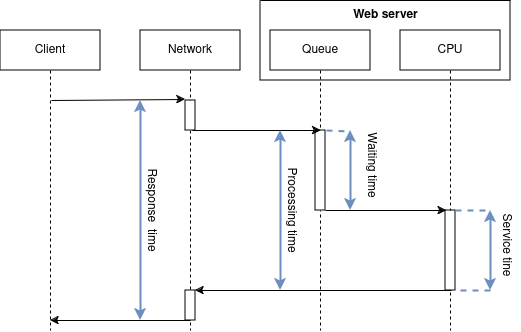We may say that response time equals to the time in the system, if we consider network as part of the system and the networking time is included into service time. We may say that processing time equals to the time in the system, if the network between client and server is not considered as a part of the system and the CPU’s time spent for the network IO is tiny comparing to the CPU time spent for computation of the response. In general, a correspondence between queuing theory concepts and the real system metrics depends on a tool at hand. Always pay attention to what exactly is measured!

In this article response time means the queueing theory’s time in the system.

Queuing theory: system utilization

Let’s start from the simplest possible model and increase the model complexity step by step to consequently uncover important patterns and properties. First of all, let’s assume what happens if both service time and inter-arrival time are constant. When the arrival rate is less or equal to the processing rate, request processing starts as soon as a new request arrives and finishes before the next request arrives, so the queue length is always zero. Response time equals to the service time.

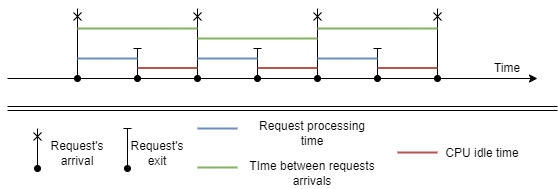
Once the arrival rate becomes greater than processing rate, the queue starts to grow infinitely. In this case, response time also tends to infinity.

Utilization shows what part of the time the system is busy in average. We use greek letter rho($(\rho$)) to denote it. We may express utilization as the ratio of the arrival and processing rates: $$ \rho = \frac{\lambda}{\mu} $$ Let’s check an example. When system is able to process 10 requests per second, while it has only 5 incoming requests per second, it’s obvious that the half of the time it has nothing to do, so the utilization rate is 50%.

Queuing theory: queues root cause

Time to make the model more complex. Imagine, that all the requests are the same, hence the processing time is constant, but now, requests arrive with some random intervals. The requests arrival rate is less than processing rate. The system has only one server, so the only one request can be processed at any point of time.

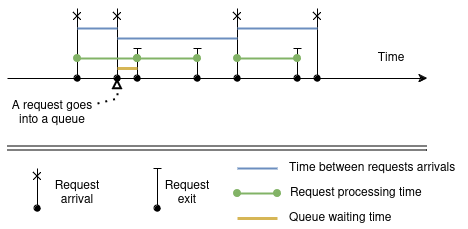
Given the $(\lambda~<~\mu$) constraint, random intervals between two consequent requests arrivals leads to queueing.

What are the possible system states in this case? 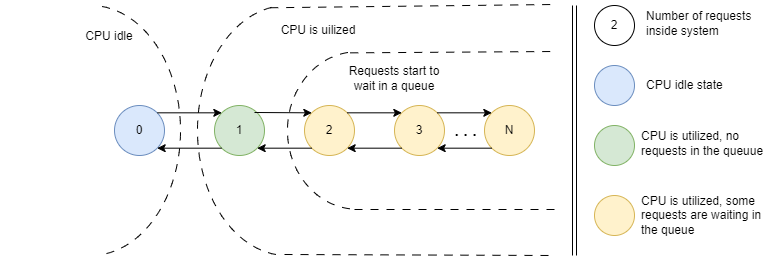First state is when there’s 0 requests in the system; it does nothing. When request arrives while the system is in this state, the response time equals to the service time: $$ T_{response} = T_{service} $$ Second state is when there’s a single request in a system. The system is busy with request processing, but there’s no queue of waiting requests yet. If a new request arrives when the system is in this state, it’s put into the queue. The response time for a new request consists of a time spent in the queue and the service time. The time spent in the queue depends on how much time left to finish work for the request is being processed by the server. We may estimate the response time for a single request in the queue as the following: $$ T_{service} < T_{response} \le 2*T_{service} $$ The third possible state is when there are two or more requests in the system when a new request arrives. One request is being processed by the server, while all other requests wait in the queue. In this case, the response time for the third and subsequent requests is: $$ N_{queue}*T_{service} < T_{response} \le (N_{queue}+1)*T_{service} $$ $(N_{queue}$) is the number of requests in a queue including the one that just arrived.

So, the response time increases very fast once requests start to queuing. Even when there’s only single request in the queue at the new request arrival its response time at least doubles! The average response time of the system is highly impacted by the average number of requests in the queue it has. How likely new request at the arrival sees a busy system with multiple requests already waiting in the queue?

When inter-arrival interval is random, the system utilization gains additional meaning. We may consider it as a time-average probability that a request at the arrival sees the system busy with processing of another request. So, the lesser utilization is the lesser expected queue length is as well. Let’s add more details to our current model to get some quantitative metrics.

Inter-arrival interval and exponential distribution

If the service time is still constant, the main factor impacting time requests spent in the queue and, consequently, response time is the distribution of the time intervals between requests arrivals. So, we have to answer 2 questions here: what is the shape of that distribution and what are its parameters. Let’s quote some parts of Erlang’s works here to answer this very important question.

Let’s assume that requests arrivals are independent. There’s no greater probability that request arrive at one particular moment comparing to any other moment. Also, there’s n requests in average over the time interval a. The $(\frac{na}{r}$) is the probability of having one call during the time $(\frac{a}{r}$) when $(r$) is infinitely great. Let’s stop here for a moment. As $(r$) tends to infinity, the time interval we’re analyzing tends to zero. So, we’re trying to estimate probability of receiving one request at specific point of time! There are no simultaneous requests, as the time interval is infinitely small. The probability to receive zero requests during the $(\frac{a}{r}$) interval is $(1-\frac{na}{r}$). Hence, the probability to receive zero requests during the whole a interval is: $$ P_0 = \lim_{r\to\infty} (1-\frac{na}{r})^r = e^{-na} $$ The power of r in the previous formula comes from the rule of joint probability of events.

What is the probability of having exact $(x$) requests during some time interval? Let’s divide interval a into r equal parts. We need to estimate joint probability of having exact $(r-x$) intervals where no requests arrive, and having x intervals where we receive 1 request. 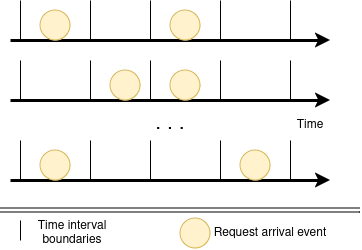It’s important to notice, that there are $(C^{r}_{x}$) combinations of such intervals.

$$ P_x = \lim_{r\to\infty}C^{r}_{x} * (\frac{na}{r})^x * e^{-(\frac{na(r-x)}{x})} = \frac{(na)^x}{x!}e^{-na} $$

Let’s introduce (\lambda=na) to denote an average number of requests arriving during the time a.
$$ P_x=\frac{\lambda^x}{x!}e^{-\lambda} $$

The formula above is Poisson Distribution that represents the probability to see exactly x events during some time interval if there’s (\lambda) events in average over this interval. However, the exact time when events occur is unknown. To return to our queueing model, we need to move from the distribution of the number of requests to the distribution of inter-arrival times. Arrivals are independent and arrival rate doesn’t change over time. Hence, everything that’s true about time interval from some “zero point” to the first event is also true for time between any two consequent events. Imagine that no request arrived yet, and we’re dividing the timeline by two parts with point T. The probability that first request arrives in a time greater than T is equal to the probability of seeing zero events over time [0, T]: $$ P_{T_{arrival}>T} =\frac{(\lambda T)^0}{0!}e^{-\lambda T} = e^{-\lambda T} $$ In this case, we may denote the probability that first request arrives in a time less or equal to T using the complement rule: $$ P_{T_{arrival} \le T} = 1 - e^{-\lambda T} $$ The formula above is the CDF of the exponential distribution.

In other words, if arrivals are independent, then the distribution of inter-arrival intervals is always exponential.

On the diagram below horizontal lines shows the constant service time and the red curve is the exponentially distributed inter-arrival time. If the inter-arrival time is less than service time, then new request gets directly into the queue. 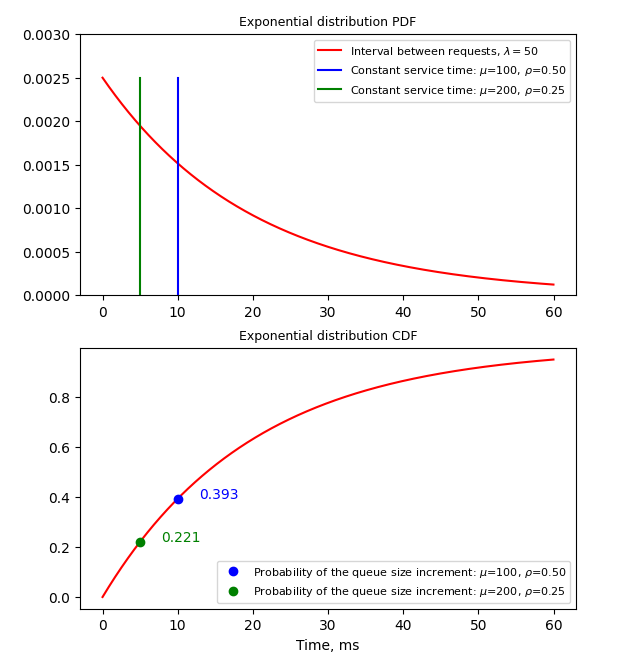The peculiarity of exponentially distributed arrivals is that even at low utilization levels the probability of the queue size increment at new request arrival is high enough. Consider the 25% utilization case. There’s a $(0.22^2=0.048$) probability to see at least one requests in the queue and $(0.22^3=0.011$) probability to have a queue of 2 consequent requests. Or in other words, for 1% of requests the response time is at least two times longer than service time.

The heavy tail of the response time distribution is inevitable if the inter-arrival time follows exponential distribution. Still, it’s possible to make outliers’ absolute value of response time less by making the service time less

How adequate is to use exponentially distributed time between arrivals for typical web-application? If users access only single page of the application and this results in a single request to a back end, the model describes the real process exactly. If users access multiple pages in a row, or a single page load requires multiple calls to a back-end, the first assumption about independence of request arrivals is not true anymore. Once server receives a first request, it also shortly receives several additional requests with a very small delay between them. Or, in other words, second and subsequent requests have a higher probability to spend some time in a queue. Is the model based on the exponential distribution of inter-arrival times still useful in these circumstances? Sure! The trends and patterns it allows to grasp stay the same, still it’s important to remember that in this case the real response time would be higher than the theory predicts.

Random service time and the Pollaczek–Khinchine formula

The constant service time is a very rare case. Usually all requests are different, so it’s reasonable to assume that their processing takes different amount of time. On the real servers, the CPU time required to process some request is usually less than the wall-clock time that request processing actually takes. This happens because request processing may be temporarily interrupted by any other task. In other words, CPU sharing policies lead to additional variance of the service time.

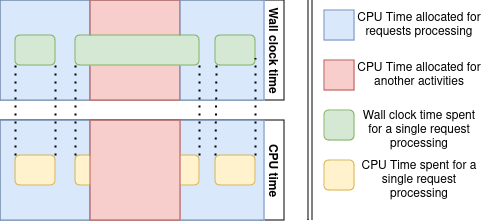
In the queuing theory, a system that consists of a single server that processes requests with exponentially distributed arrivals and any distribution of the service time is denoted as M/G/1.

We may express the expected response time of the system as a sum of the expected service time and the expected waiting time. The expected service time comes directly from the service time distribution, while the waiting time depends on the expected queue length. We’re going to focus on waiting time only because the service time’s part of the average response time is constant, and it doesn’t depend on the system utilization, while the waiting time does. Let’s do some math to evaluate expected waiting time:

$$ E[T_{waiting}] = E[N_Q] * E[T_{service}] + \rho * E[T_{service~time~excess}],~~{where} $$

• $(E[T_{waiting}]$) is expected waiting time in the queue
• $(E[N_Q]$) is expected number of requests in the queue
• $(E[T_{service}]$) is expected value of the request service time
• $(\rho$) is the system utilization that equals to the probability of the server being busy
• $(E[T_{service~time~excess}]$) is the expected value of the service time excess

The service time excess is the amount of the time left to finish processing of the current request.

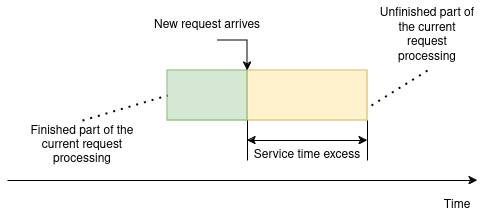
The key to the next equation transformation is that we may treat the server’s queue as independent system with known requests arrival rate $(\lambda$) and the known expected response time, that equals the queue waiting time. The arrival rate for the server’s queue is the same as for the whole system and the request processing time equals to the expected time spent in the queue. Let’s use Little’s Law to express the expected queue length:

$$ E[N_q] = \lambda * E[T_{waiting}] $$

Now we may substitute the expected queue length into the initial formula: $$ E[T_{waiting}] = \lambda * E[T_{waiting}] * E[T_{service}] + \rho * E[T_{service~time~excess}] $$

Another way to express system’s utilization is to use requests arrival rate and expected processing time: $$ \rho = \lambda * E[T_{service}] $$

Using the utilization formula from the above, we receive: $$ E[T_{waiting}] = \rho * E[T_{waiting}] + \rho * E[T_{service~time~excess}] $$

Now, let’s get equation for $(E[T_{waiting}]$) using very basic equation transformations: $$ E[T_{waiting}] = \rho * E[T_{waiting}] + \rho * E[T_{service~time~excess}] \Leftrightarrow $$

$$ E[T_{waiting}] - \rho * E[T_{waiting}] = \rho * E[T_{service~time~excess}] \Leftrightarrow $$

$$ E[T_{waiting}](1 - \rho) = \rho * E[T_{service~time~excess}] \Leftrightarrow $$

$$ E[T_{waiting}] = \frac{\rho}{1 - \rho} * E[T_{service~time~excess}] $$

The derivation of the expected service time excess is quite long, so let’s use a ready formula: $$ E[T_{service~time~excess}] = \frac{E[T_{service}^2]}{2E[T_{service}]}, where $$

$(E[T_{service}^2]$) is the second moment of the processing time distribution or the variance of that distribution $(Var(T_{service})$).

That finally gives us the Pollaczek–Khinchine formula:

$$ E[T_{waiting}] = \frac{\rho}{1 - \rho} * \frac{Var(T_{service})}{2E[T_{service}]} = \frac{\lambda * Var(T_{service})}{2(1-\rho)} $$

Utilization, service time and the response time.

To make things easier to imagine, we’re going to use the coefficient of variation instead of variance: $$ CV(T_{service}) = \frac{\sqrt{Var(T_{service})}}{mean(T_{service})} $$ Coefficient of variation is another way to evaluate how much each specific measurement or observation is expected to differ from the mean value. High CV values are not rare in practice, for example exponential distribution has CV of 100%. The curves on the diagram below represent how the average queue waiting time depends on the utilization. Different curves correspond to different coefficients of variation of the service time distribution. 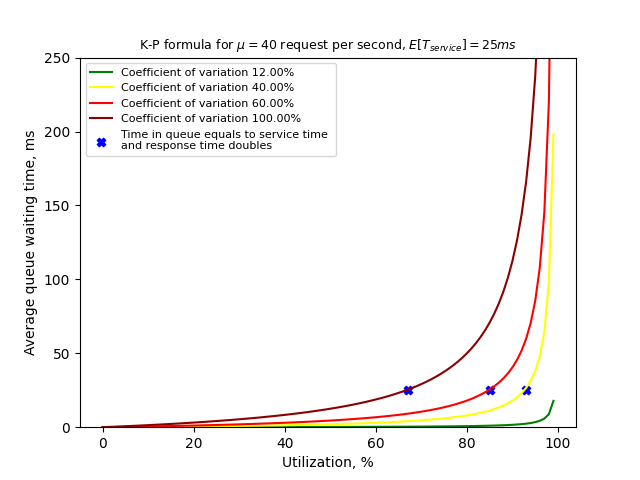This diagram demonstrates important practical aspect. While the waiting exponentially depends on the utilization, it’s the variance that defines utilization level at which average waiting time starts to hit the skies. So, the higher is the variance coefficient of the service time, the more servers are required to keep utilization level low and, hence, average waiting and response times low. Obviously, the more servers are required the more infra costs. The variance of the service time could be caused by:

1. Remote calls. A remote service’s response time distribution could have heavy tail that leads to heavy tail of the service time. Usually, distributions with heavy tails have high variance.
2. CPU sharing policies. Sharing CPU between multiple processes introduces random delays into the request processing. Hence, the variance increases.
3. Algorithms with time complexity greater than O(log(N)).

It’s worth to mention, that high average response time at low utilization levels could be also caused by the nature of the inter-arrival distribution. What would be the average queue size in the following scenario: 10 requests arrive simultaneously, then pause, then 10 more requests arrive simultaneously, then pause and so forth.

Few very simple things that could help to decrease the variance of the service time, and hence, improve the response time:

1. Use asynchronous IO, if request processing requires remote calls
2. Align the number of worker threads with the number of CPU cores allocated to a workload
3. Configure CPU cores affinity for a workload. It’s possible in Linux and Kubernetes.

There are two ways to reduce utilization. First is to send fewer requests, second is to process requests faster. The diagram below shows how the average response time depends on the average service time. 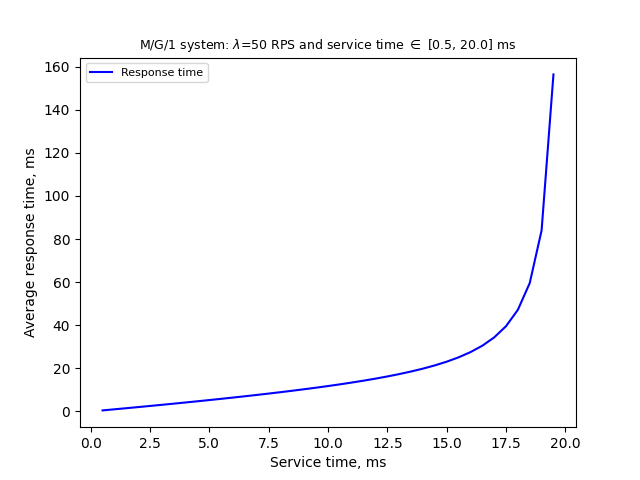If some improvement reduces processing time by 50% and the initial utilization level is 80%, you may expect exponential improvement of the response time, while if the initial utilization level is 40%, the gain is mostly linear.

So far we reasoned about systems that have only single CPU core, however modern computers have multiple cores. Simulation is the easiest way to get performance metrics for multicore systems, still the current model could be used for rough estimations and search of potential system performance improvements.

If you’re interested in the second part about multi-core systems, connect on LinkedIn to not miss it!

Notes and references

1. Kingman’s formula allows to evaluate systems when the inter-arrival intervals have any distribution.
2. THE THEORY OF PROBABILITIES AND. TELEPHONE CONVERSATIONS by A.K. Erlang.
3. Relationship between poisson and exponential distribution
4. An interesting paper from VMWare, that shows how the CPU affinity impacts the performance metrics of the workload deployed into kubernetes cluster. See “Tuned Bare-Metal Results” section!
5. Performance Modeling and Design of Computer Systems: Queueing Theory in Action by Mor Harchol-Balter.